Modelling simple finite state machines in F#

State machines are found everywhere, whether they are fleshed out initially as such is a different matter.

In an application it's common to see different states being represented as an enum, and the transitions replace the current state with the next based upon some logic.

If we take an email address as a real world example, the application must be capable of representing an email address in both verified and unverified states.

We could represent it like this...

type EmailAddress = {
    EmailAddress: string;
    IsEmailVerified: bool;
}

Using a bool flag. Nothing wrong here right? But this doesn't help us express our state in the domain very well. What happens when the record needs to represent different data depending upon it's state? For example:

type EmailAddress = {
    EmailAddress: string;
    IsEmailVerified: bool;
    VerifiedDate: DateTime option; // only needed if email is verified
}

The type becomes less focused, and even more difficult to construct. Instead of saying what an EmailAddress is it's starting to say what an EmailAddress can be dependent upon state.

There is another way to do this. The F# type system is advanced enough to allow us to represent these states directly - as discriminated unions.

module EmailAddress =
    open System

    type EmailAddress = string
    type VerifiedEmailData = EmailAddress * DateTime
    type T =
        | UnverifiedEmail of EmailAddress
        | VerifiedEmail of VerifiedEmailData

Much better, now an unverified email doesn't have to concern itself with a VerifiedDate or any other fields that might be there.

So this is a very simple example, we only have 2 states; Unverified and Verified. An email address must be in 1 of either of the 2 states. It's either verified, or it is not.

Transitions

Now we have the states fleshed out, we need to define transitions (or events) which have the responsibility of governing the states, in other words; from state A to state B. So using the email example, we really only have one transition, and that's an UnverifiedEmail becoming a VerifiedEmail.

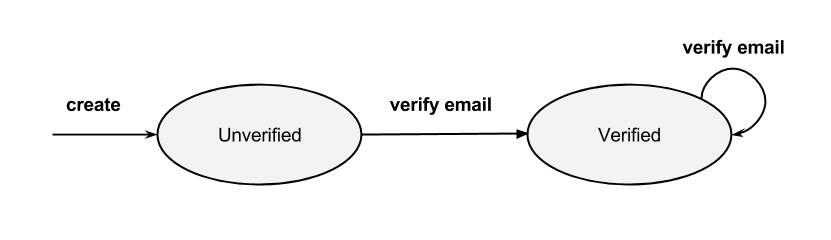
module EmailAddress =
    
    ...

    let create email = UnverifiedEmail email

    let verify email date =
        match email with
        | UnverifiedEmail email -> VerifiedEmail (email, date)
        | VerifiedEmail _ -> email

You can see how the verified transition handles a VerifiedEmail by just returning it.

We also need a way to create an email address, but that's easy, a new email always begins it's life as unverified.

Before continuing, let's take a closer look at that verify function.

verify : EmailAddress.T -> DateTime -> EmailAddress.T

You might be wondering why our verify function doesn't just take an Unverified email directly and have done with the match?

verify : T.Unverified -> DateTime -> T.Verified

We could do this, but how would we handle the other state?
Each transition must take and return the whole state machine. Each state needs to be handled somewhere, it's best handled by the transition function rather than the caller, it's much easier to encapsulate and while also being explicit about the logic of our system. F# will also help you out on this as the compiler will warn you whenever you don't match against every possible case, win.

Stepping it up

Lets use the same principals and apply it to another real world problem. Payments.

Cards

We will need to support multiple payment types. So I'll just go ahead and put a few in for this; VISA, PayPal and a CashCard.

type CardNumber = CardNumber of string
type ExpiryDate = ExpiryDate of DateTime
type CV2 = CV2 of int
type EmailAddress = EmailAddress of string

type PaymentProvider =
    | Visa of CardNumber * ExpiryDate * CV2
    | Paypal of EmailAddress
    | CashCard of CardNumber

Transaction data

So forgetting whether this is a withdrawal transaction or not, what data do we need to make a successful payment? We should put all that into a record to contain it. All of which are very obvious:

type TransactionData = { 
    Amount: decimal;
    Provider: PaymentProvider;
    CreatedDate: DateTime
}

I'm sure there will be more but for the sake of keeping things simple i'll stick with these 3.

Defining our states

This is probably the most important part, expressing all of the different states a transaction can be in throughout the process. I've come up with 4 obvious ones which are:

• Unsigned, the unactioned state.
• Pending, the transaction is currently being processed.
• Declined, the transaction has been declined.
• Completed, the transaction has been successfully processed.

Let's write this out:

type PaymentTransaction =
    | Unsigned of TransactionData
    | Pending of TransactionData
    | Declined of TransactionData * Reason * DateTime
    | Completed of TransactionData * DateTime

The Unsigned and Pending states only require actual TransactionData. Additionally, the Declined state can also include a Reason for the failure and a timestamp. The Completed state should probably also include a timestamp.

Payment transitions

The transitions involved are simple, the payment process follows a very linear path without any deviation really. The transaction can be in only one state at any given time (which is the whole point) and all cases are handled explicitly. It's certainly helpful to look at the system more abstractly using a diagram or table.

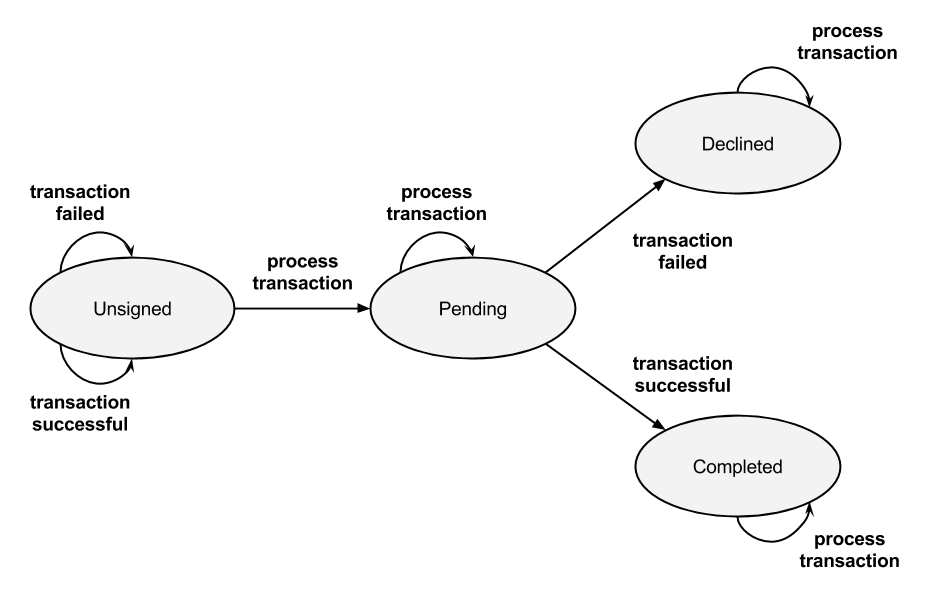
Now to write out the transitions.

let processTransaction transaction =
    match transaction with
    | Unsigned t -> Pending t
    | Pending _ -> transaction
    | Declined _ -> transaction
    | Completed _ -> transaction

let transactionFailed transaction reason =
    match transaction with
    | Unsigned _ -> transaction
    | Pending t -> Declined (t, reason, DateTime.Now)
    | Declined _ -> transaction
    | Completed _ -> transaction

let transactionSuccessful transaction =
    match transaction with
    | Unsigned _ -> transaction
    | Pending t -> Completed (t, DateTime.Now)
    | Declined _ -> transaction
    | Completed _ -> transaction

In most cases, you would probably want to handle the side cases in other ways than just returning the transaction which was passed to the function.
Especially with the Declined state, the system might allow a Declined transaction to be reprocessed - which I haven't catered for here, but would be a simple change to make.

Using it

So that's the machine done. All that's left to do is to use it. We still need a way to actually send a payment/transaction to be processed.

This is a good opportunity to use F#'s MailboxProcessor to create an agent or actor. The agent will receive transaction messages as they are sent to it and handle them however we see fit.

The main reason i'm using an actor here is they are very easy to scale and allow us to build in supervision. In a real project, I would recommend Akka.NET for such tasks.

[<AutoOpen>]
module Processor =
    type Agent<'T> = MailboxProcessor<'T>
    type PaymentResult =
        | Success
        | Failure of Reason
    type Message = PaymentTransaction * AsyncReplyChannel<PaymentResult>

    let agentRef = Agent<Message>.Start (fun inbox ->
            let rec loop = async {
                let! (msg, replyChannel) = inbox.Receive()

                (* send request to vendor etc... *)

                replyChannel.Reply Success // or Failure with a reason
                return! loop
            }
            loop
        )

module TheGraft =
    let sendPayment processor transaction =
        async {
            let pendingTransaction = processTransaction transaction 
            let! paymentResult = processor pendingTransaction
            match paymentResult with
            | Success -> 
                return transactionSuccessful pendingTransaction
            | Failure reason -> 
                return transactionFailed pendingTransaction reason
        }

    let sendPaymentUsingAgent = sendPayment (fun transaction -> 
        Processor.agentRef.PostAndAsyncReply (fun reply -> (transaction, reply)))